Multi-Armed Bandit
I finished 23rd out of 792 teams in Kaggle’s 2020 Christmas Competition.
My simple final result is only possible because of all of the time I spent experimenting and testing, but I’m glad I found something elegant.
Code on Github
Kaggle 2020 Christmas Competition
This challenge is a head-to-head version of the multi-armed bandit.
Two agents have to select from one hundred bandits, each with a random probability of giving a reward. Every time a bandit is chosen, its likelihood of giving a reward decreases by 3%. Each agent can only see their total reward, the last action from each agent, and the step count. The agent with the highest reward after 2000 steps wins.
Greedy Keras Regression Agent
Kaggle’s saved game data includes the true payout threshold for each bandit, and I trained a regressor that estimates the payout probability based on all the observed data for each bandit. My agent then predicts the payout rate for each bandit and selects the bandit with the highest expected rate.
Ultimately I think that a greedy regression approach will fail to get into the top 10 because it can only approximate the strongest agents, but someone else might prove me wrong. Many of the top teams added logic to confuse their opponents and avoid leaking information.
Data
I gathered episodes of 1200+ agents using this notebook: https://www.kaggle.com/masatomatsui/santa-episode-scraper
My game parsing is based on this, but updated to include my new features: https://www.kaggle.com/lebroschar/generate-training-data
In total I had 45 million training rows, each with my 7 features and the true payout rate.
I noticed a significant increase in strength for every 5 million rows added, and I likely could have made my agent better with even more data.
Features
This challenge gives very little data to work with, but I improved my results by supplementing the available data with pull and win streaks.
- step number
- number of pulls
- number of opponent pulls
- reward - total reward for the agent
- streak - number of times the agent has pulled this in a row
- opponent streak - number of times the opponent has pulled in a row
- win streak - number of times this agent has given a reward in a row
Model
My Keras model takes all of the known info about a single bandit and estimates its probability. I chose to make a regressor for a single bandit rather than a classifier that takes the state of every bandit because relationships between bandits shouldn’t matter, and because the actual payout probability from saved episodes makes a great regression target.
I used 7 input features, 3 hidden layers of 12 units, and one output unit with a sigmoid activation. 4 layers and 16 units also worked well. All of my models were under 1,000 parameters and trained very quickly.
Root mean error didn’t always correlate cleanly with actual performance, so I figured out the right network size through head-to-head simulation.
Model Code
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
input_layer = Input(shape=(7,))
m = Dense(12, activation='relu')(input_layer)
m = Dense(12, activation='relu')(m)
m = Dense(12, activation='relu')(m)
m = Dense(1, activation='sigmoid')(m)
model = Model(inputs=[input_layer], outputs=m)
opt = Adam(learning_rate=0.01)
model.compile(optimizer=opt, loss='mean_squared_error')
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 7)] 0
_________________________________________________________________
dense (Dense) (None, 12) 96
_________________________________________________________________
dense_1 (Dense) (None, 12) 156
_________________________________________________________________
dense_2 (Dense) (None, 12) 156
_________________________________________________________________
dense_3 (Dense) (None, 1) 13
=================================================================
Total params: 421
Trainable params: 421
Non-trainable params: 0
Agent
My agent submission loads the keras model and track bandit state in a dataframe. To choose a bandit, the agent uses the model to predict the payout rate for each bandit and picks the bandit with the highest rate.
Most of the complexity and almost all of my development time was spent fine-tuning the model, not the agent code.
Other Ideas that Worked For Me
DecisionTreeRegressors can also predict the real bandit probability quite well.
I got the best results with min_samples_leaf=100 and no depth limit.
A Keras + Decision Tree Ensemble from the two models performed worse in my local testing but did well on the leaderboard. Maybe the ensemble is more robust against unknown opponents? I eventually dropped the ensemble idea when my Keras models became much more powerful than decision trees.
Ideas that Didn’t Work
I turned my regressor into a classifier by convolving my regression weights across all 100 bandits and then training it with policy gradients. My best classifier is currently at 970 on the LB, but my simple RL approach was never enough to beat my regressor.
I considered a DQN but decided against it because the “actions” in this environment work exactly the same in each state, so learning action values seemed like the wrong approach when the true bandit probabilities are known from stored game episodes.
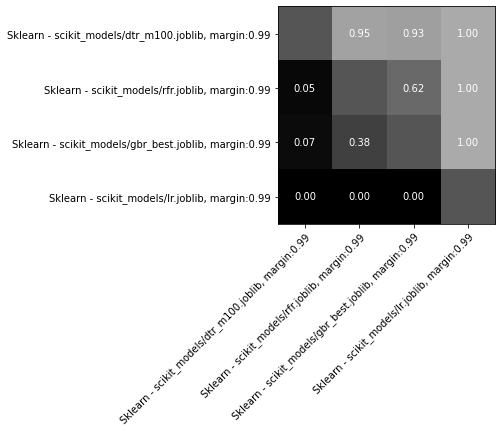
Other sklearn regressors fit the dataset well - random forests even had lower error that decision trees - but only decision trees performed well in actual simulation. I’m not sure why random forests showed such a huge gap between dataset and environment performance.
These round robin results show decision trees easily beating random forests, gradient boosting, and linear regression.
Sources
Bayesian UCB
Thompson Sampling
Training data collection
Decision Tree Regressor
Ray support
Pull Vegas