Satisfactory Optimizer

Using Google’s OR-Tools to find optimal production ratios in Satisfactory.

Code on Github

Data taken from SatisfactoryTools

Satisfactory

Satisfactory is a game of automation. You start by building machines to extract raw resources, then you combine resources and items into increasingly complex products. A Miner produces Iron Ore, and then a Smelter turns Iron Ore into Iron Ingots etc.

source

Recipes

Each construction machine takes input items and creates new items based on a specified recipe. For example, the default Iron Ingot recipe turns 30 Iron Ore into 30 Iron Ingots every minute.

More advanced items can have up to four input items, and each recipe has unique input/output ratios, speeds, and by-products to consider. Here’s a chart showing the steps to build a late-game item.

source

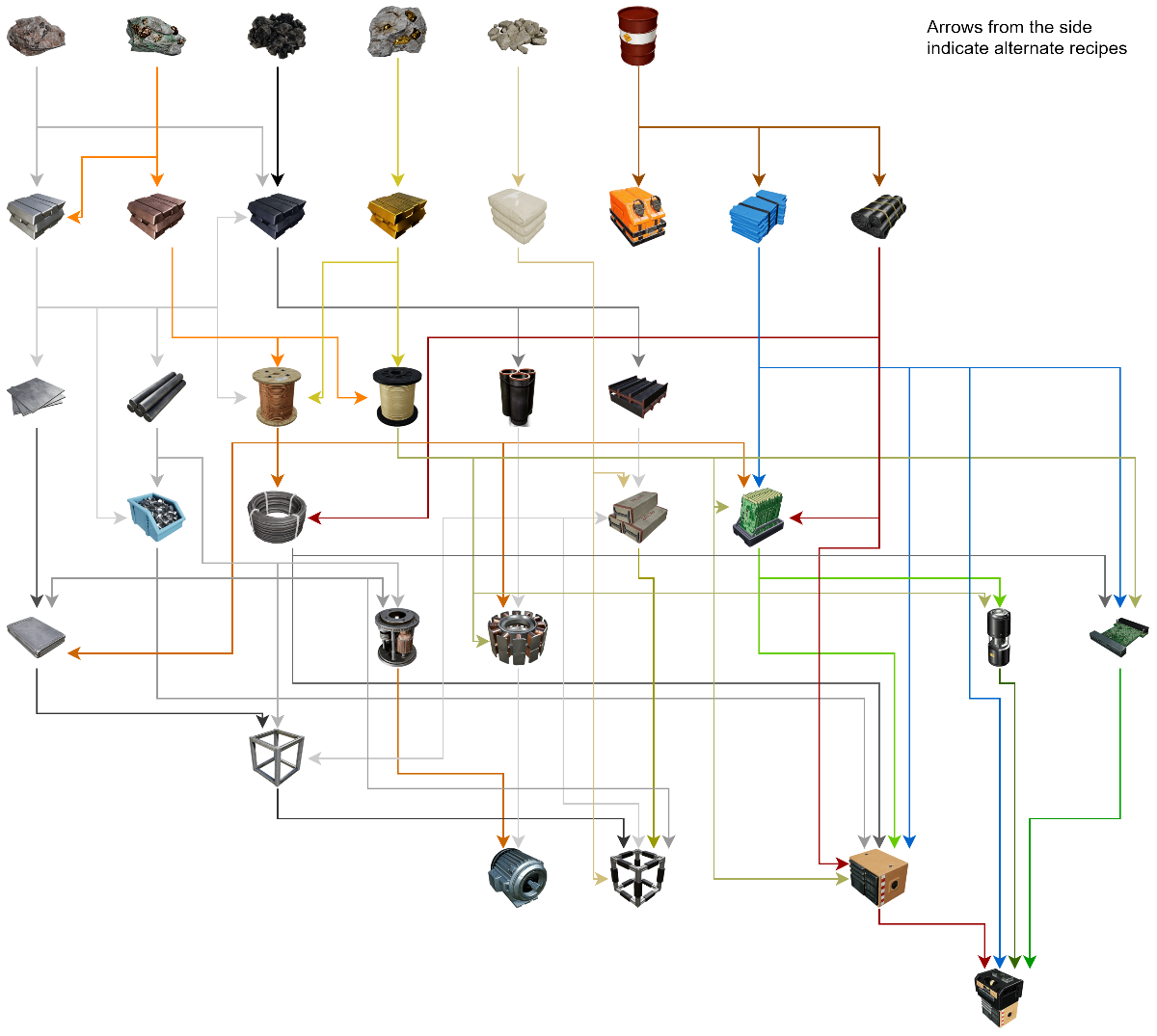
Quite a lot to remember when building a factory!

Alternate Recipes

To add even more complexity, many items have alternate recipes that may boost production depending on which starting resources are more plentiful. For example, there are three Iron Ingot recipes:

• Iron Ingot: 30 Iron Ore to 30 Iron Ingots
• Pure Iron Ingot: 35 Iron Ore and 20 Water to 65 Iron Ingots
• Iron Alloy Ingot: 20 Iron Ore and 20 Copper Ore to 50 Iron Ingots

Which recipe is the best? It depends on which resources are nearby. If you have excess water/copper, and a shortage of iron, then the alternates will help.

This Satisfactory Optimizer takes all alternate recipes into account and gives an optimal factory setup based on your available materials.

Dependencies

Install OR-tools with Pipenv
pipenv install

Linear Optimization

I modelled the recipe production ratios as a linear programming problem.
A linear programming problem consists of decision variables, constraints, and an objective function.
The optimizer modifies the decision variables to maximize the objective function while satisfying its constraints.

Decision Variables

We need to know how many machines should produce each recipe. Therefore, the recipe assignments are the decision variables.

x_r = # of machines producing recipe r

x_r is a non-negative real number.

Objective Function

We want to create as many desirable products as possible, so the objective function is the score of each component multiplied by the total produced. In order to eliminate extraneous recipes that don’t contribute to the final score, each recipe incurs a small penalty.

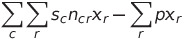
where s_c is the score for component c,
n_cr is the quantity of c produced by a single machine with recipe r,
and p is a small, positive penalty.

n_cr will be negative if r consumes c as an input.

Constraints

For this problem, the only constraint is that each component has a non-negative quantity, otherwise the optimizer could use recipes without having prerequisite materials.

For each component c,

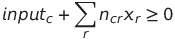
where input_c is the specified input amount for component c.

OR-Tools

Now that recipe optimization is modelled as a linear programming problem, it’s time to plug it into OR-Tools. Since this is a linear programming problem, I used the GLOP linear solver.

from ortools.linear_solver import pywraplp

solver = pywraplp.Solver.CreateSolver('GLOP')

Decision Variables

The solver needs to know about each decision variable x_r, so I created a dictionary with a variable for each recipe.

recipe_vars = = dict([(r.name, solver.NumVar(0, 100, r.name)) for r in recipes])

The value of each variable is between 0 and an arbitrary max value, I chose 100.

Objective Function

To calculate the objective, I calculate the total score of the outputs for each recipe and add them together. I also subtract a small recipe cost to remove extraneous recipes.

objective = solver.Objective()
for i, recipe in enumerate(recipes):
    recipe_contribution = sum([recipe.component_net_quantity(c) * s for c, s in outputs.items()])
    recipe_contribution -= 0.01
    objective.SetCoefficient(recipe_vars[recipe.name], recipe_contribution)

Constraints

Each component is constrained such that its total value from all recipes and inputs is non-negative.

for component in components:
    min_value = -inputs[component] if component in inputs else 0
    ct = solver.Constraint(min_value, 10000, component)

    # add the contribution of each recipe
    for i, recipe in enumerate(recipes):
        ct.SetCoefficient(recipe_vars[recipe.name], recipe.component_net_quantity(component))

Usage

Example resource calculation in satisfactory.py

1. Load recipes from the data file. For simplicity this example only uses default recipes.
2. Specify the available resources in units/minute.
3. Give a positive score to components you want to create.
4. Send the recipes, inputs, and outputs to the optimizer

recipes = load_recipes()
default_recipes = [r for r in recipes if not r.alternate]

inputs = {
    "Iron Ore": 60
}

outputs = {
    "Reinforced Iron Plate": 1
}

optimizer = Optimizer(default_recipes, inputs, outputs)
optimizer.optimize()

Then run

pipenv run python satisfactory.py

Output:

Solution:
Objective value: 4.93

Recipes Used:
Iron Ingot: 2.00
Reinforced Iron Plate: 1.00
Iron Plate: 1.50
Iron Rod: 1.00
Screw: 1.50

Inputs Remaining:
Iron Ore: 0.00

Produced Components:
Reinforced Iron Plate: 5.00

Recipes Used shows how many machines need to run each recipe.
Inputs Remaining shows which resources run out first and limit production.
Produced Components shows all the produced components, not just those with a score.

Advanced Example

I originally made this to optimize my fuel setup because oil refining has lots of by-products and complex alternate recipes. Let’s see how it does on a more complicated example.

Assume 300 oil per minute, all recipes are unlocked, and we want to produce as much energy as possible. In order to optmize energy production, set each output’s score to its in-game energy value.

inputs = {
    "Crude Oil": 300,
    "Water": 800,
    "Coal": 533.33,
    "Sulfur": 533.33
}
outputs = {
    "Fuel": 600,
    "Turbofuel": 2000
}

This result matches the optimal fuel setup guide!

Recipes Used:
Alternate: Diluted Packaged Fuel: 13.33
Alternate: Compacted Coal: 21.33
Alternate: Heavy Oil Residue: 10.00
Turbofuel: 35.56
Packaged Water: 13.33
Unpackage Fuel: 13.33

Inputs Remaining:
Crude Oil: 0.00
Water: 0.00
Coal: 0.00
Sulfur: 0.00

Produced Components:
Polymer Resin: 200.00
Turbofuel: 666.66

Next Steps

Next I could update this take power consumption into account, but with my optimal fuel setup I don’t think I’ll run out of power for a while.